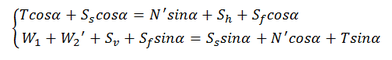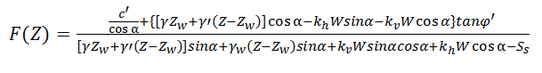Infinite Slope v. 3.0 theoretical basis.
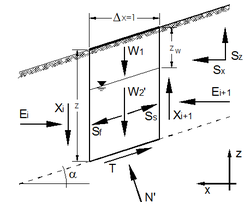 Free body scheme of a vertical slice.
Hypothesis
The well known 'Infinite slope' model (Skempton, 1957) is a simple mechanical approach based on the following assumptions: - slope extent is undefined or much larger than the depth of potential slip surface; - slope angle is constant and not too large; - soil characteristics are homogeneous along the slope direction; - failure or slip surface is parallel to the slope's ground surface; - rigid-perfectly plastic constitutive law; - Mohr-Coulomb's failure criterion on the slip surface; - seismic conditions are simulated by separated pseudo-static components of the seismic force; - seepage has a direction parallel to the slope or doesn't take place; - theory of unsaturated soils is not taken into account. For a complete list of the features see here: Analytical formulation Studying the equilibrium of the above free body diagram through the following system of equations: The below equation is obtained by considering the definition of the Factor of Safety as Tf/T:
where:
- α is the slope angle; - Z the depth of the potential slip surface; - Zw the depth of the groundwater free surface flow from the ground surface; - γ the unsaturated unit weight above the groundwater free surface; - γsat the saturated unit weight under the groundwater free surface; - γ' the effective unit weight under the groundwater free surface; - c' cohesion of soil (on the potential slip surface at depth Z); - φ' shear strength angle (on the potential slip surface at depth Z); - W the total weight of the slice; - kv the vertical pseudo-static seismic coefficient; - kh the horizontal pseudo-static seismic coefficient; - Ss the stabilizing force (supported by the shear pile walls). Limits of applicability The model is suitable to perform stability analyses of slopes that satisfy the above hypothesis, which means soil masses constituted by layers parallel to the slope and in any case where the failure surface is expected or known to be planar and parallel to the slope. For slopes constituted of homogeneous fine grained soils this model is often not suitable to obtain a correct interpretation of failure mechanisms (circular and not planar) and isn't able to evaluate a correct factor of safety for the slope. If groundwater flow is present seepage direction must be parallel to the ground surface. Validation and disclaimer This software has been verified by manual calculations and has been compared to other commercial codes giving a good agreement of the results. Nevertheless, the author cannot assume any responsibility about the use of its results. |
|